Hàm căn bậc 2 được sử dụng trong Excel là hàm SQRT. Hàm Excel này được giới thiệu đầu tiên trên Excel 2010 và được phân loại là hàm toán học, được sử đụng để trả về căn bậc 2 của một số dương. Trong bài viết dưới đây Macstore sẽ giới thiệu chi tiết cho bạn về cú pháp hàm căn bậc 2 trong Excel SQRT cũng như cách sử dụng hàm này.
Nội dung chính
Hàm căn bậc 2 trong Excel
Hàm SQRT trong Excel là hàm phổ biến nhất được sử dụng để tính căn bậc 2 của một số trong bảng tính Excel. Bên cạnh đó hàm SQRTPI cũng được sử dụng để tính căn bậc 2 của một số nhân với số pi.
Công thức hàm SQRT trong Excel
Cú pháp hàm SQRT, hàm căn bậc 2 trong Excel có dạng như dưới đây:
=SQRT(number)
Trong đó hàm SQRT sử dụng tham số:
– Number (tham số bắt buộc): là số mà chúng ta muốn tìm căn bậc hai. Tham số này phải là số thực dương, nếu không hàm Excel căn bậc 2 sẽ trả về thông báo lỗi.
Cách sử dụng hàm căn bậc 2 trong Excel
Dưới đây là một số ví dụ để bạn dễ hình dung cách sử dụng hàm SQRT, hàm căn bậc 2 trong Excel:
Ví dụ 1
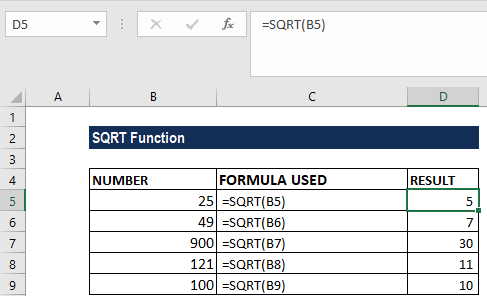
Giả sử cho các giá trị sau đây, nhiệm vụ của bạn là tính căn bậc 2 của các số, các giá trị này lần lượt là: 25, 49, 900, 121, 100.
Cú pháp, công thức hàm căn bậc 2 Excel được sử dụng có dạng như sau:
= SQRT(tham chiếu).
Kết quả trả về có dạng như dưới đây:
Ví dụ 2
Trong trường hợp nếu tham số number hay số mà chúng ta cần tính căn bậc 2 là một số âm thì hàm SQRT sẽ trả về giá trị lỗi là #NUM!. Điều này là bởi vì căn bậc của một số âm không tồn tại.
Tuy nhiên chúng ta có thể lấy căn bậc 2 của một số âm như thể nó là một số dương bằng cách sử dụng hàm ABS.
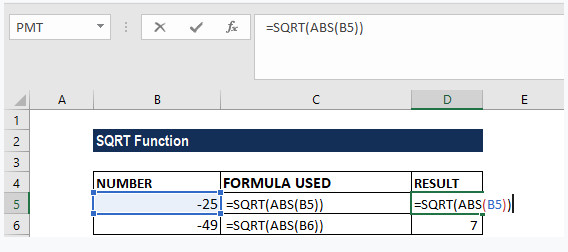
Giả sử cho dữ liệu như trong bảng dưới đây:

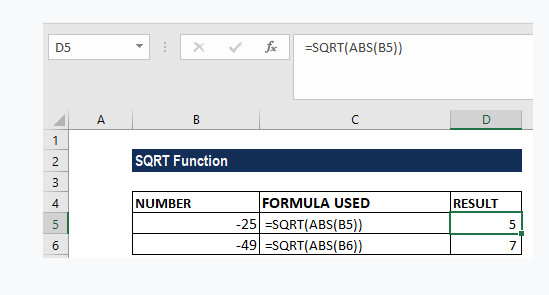
Để tìm căn bậc 2 của các giá trị, chúng ta sử dụng công thức hàm SQRT có dạng như dưới đây: = SQRT(ABS (ref)):
Khi đó kết quả trả về sẽ có dạng như sau:
Hàm SQRTPI trong Excel
Hàm SQRTPI trong Excel tương tự như hàm SQRT, chỉ có điều hàm SQRTPI nhân thêm với số pi để cho ra kết quả. Cách sử dụng hàm SQRTPI cũng tương tự hàm SQRT.
Viết số mũ trong Excel
Cách nhanh nhất để viết số mũ trong bảng tính Excel là sử dụng phím tắt. Trong đó:
- Mũ 2: Nhấn và giữ đồng thời các phím: Alt+ 0 + 1 + 7 + 8.
- Mũ 3: Nhấn và giữ đồng thời các phím: Alt+ 0 + 1 + 7 + 9.
Hàm POWER tính căn bậc 2
Ngoài hàm SQRT, Excel còn được bổ sung thêm hàm Power, cũng được sử dụng để tính căn bậc 2 của một số trong bảng tính.
Cú pháp hàm căn bậc 2 Power trong Excel có dạng như dưới đây:
= POWER (số n, power)
Trong đó:
- Tham số đầu tiên (số n) có thể là số thực hoặc tham chiếu đến ô cần tính.
- Tham số power là lũy thừa, số mũ mà số n được nâng lên.
Hàm Power trả về lỗi #NUM nếu một trong số các tham số mà chúng ta sử dụng là số âm.
Khác với SQRT, hàm Power Excel còn được sử dụng để tính căn bậc 2, căn bậc 3 và thậm chí là căn bậc N.
Một số lưu ý khi sử dụng hàm căn bậc 2 trong Excel
- Hàm SRQT trả về lỗi #NUM! nếu tham số, số cần tìm căn bậc 2 đã cho là một số âm.
- Chúng ta có thể sử dụng hàm SQRT kết hợp với các hàm Excel khác như ABS, ROUND, ROUNDUP và ROUNDDOWN.
- Hàm SQRT về cơ bản hoạt động tương tự hàm POWER, chỉ có điều hàm POWER hoạt động như số mũ trong phương trình toán học.
Trên đây là tất tần tật cú pháp hàm căn bậc 2 trong Excel cũng như cách sử dụng hàm như thế nào. Hy vọng sau bài viết trên đây của Macstore sẽ giúp bạn làm chủ được hàm Excel này.
Xem thêm các bài viết cùng chủ đề:
- Hàm Countifs trong Excel
- Hàm Dsum trong Excel
- Hàm Average trong Excel
- Hàm Right trong Excel




